Let's learn how to write and graph interval notation.

What is an Interval Notation?

Interval notation is a way of writing solutions to algebraic inequalities. You may recall that inequalities are relations that compare non-equal mathematical expressions. The four inequality signs are: less than (<), greater than (>), less than or equal (≤), and greater than or equal (≥). Here are some examples of inequalities.

  • x > 4
  • x+5 > 3
  • 4 > 2
  • 3-x > 1

Inequalities like the examples above usually have many to infinite solutions; two easy ways to denote these solutions are by graphing them on the number line and using interval notation. An interval refers to the numbers between two points.

The interval between 1 and 5 (meaning 2, 3, 4) is expressed in the interval notation: (1, 5). Interval notation only includes the lower-bound (beginning) and upper-bound (ending) numbers or points, which are 1 and 5, respectively. Note that 1 and 5 are not included in the sample interval, as signified by the use of parentheses ().

To better understand graphing and interval notation, see the illustration below:

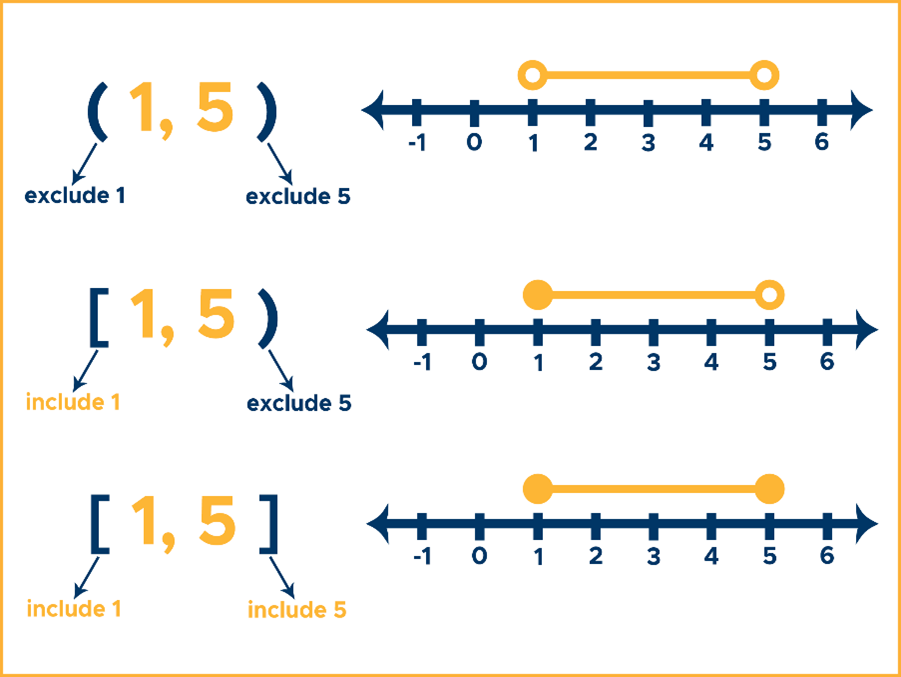
Interval Notation 1 to 5

Notice that the graph of (1, 5) used two open dots at 1 and 5, meaning 1 and 5 are excluded in the solution set, while the graph of [1, 5] used two closed dots at 1 and 5, meaning 1 and 5 are included in the solution set.

How to Write the Interval Notation of Solutions to Inequalities:

Step 1. Graph the solution set on the number line. Use an open dot (○) at the boundary point/s excluded in the solution. Use a closed dot (●) at the boundary point/s included in the solution.

Step 2. Write the interval notation beginning with the lower-bound then the upper-bound. Use square brackets ([ ]) to indicate the inclusion of the boundaries in the solution, or parentheses ( ) to indicate their exclusion.

NOTE: Infinities (-∞, +∞) are always enclosed with a parenthesis. Also, solution sets can have one square bracket and one parenthesis on either side, depending on the inclusion or exclusion of the boundaries.

For example, look at the image below.

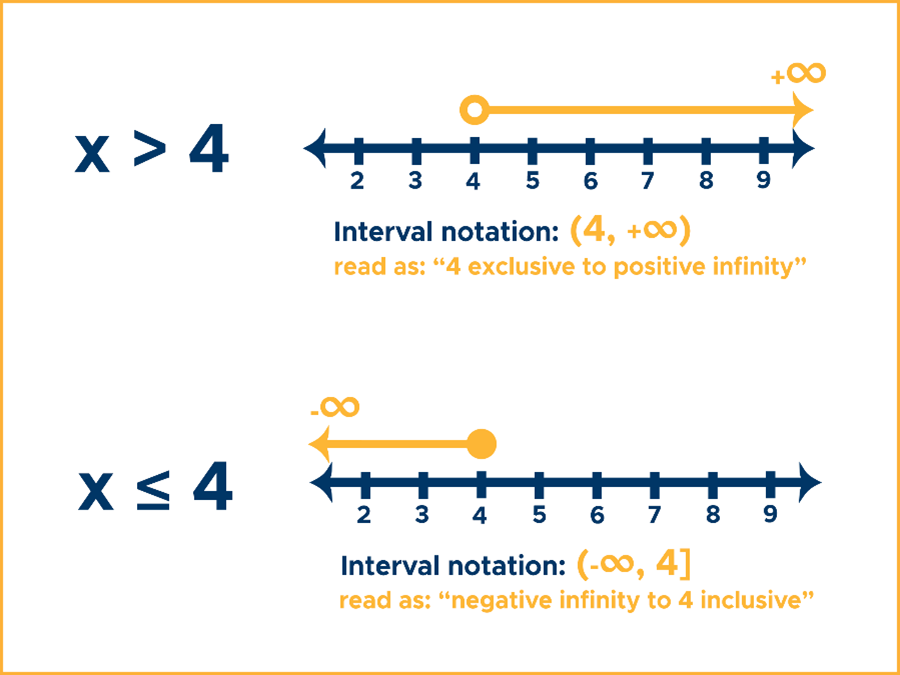
Interval Notation Graphs x > 4, x < 4

x > 4
Solution:
Step 1. Graph the solution. Use an open dot at 4 and shade all real numbers greater than 4. Put positive infinity above to indicate that the solution set is unbounded to the right of the number line (or all positive real numbers).
Step 2. Write the interval notation using a parenthesis because the lower-bound (4) is not included, then put positive infinity as the upper-bound, which is automatically enclosed with a parenthesis.
Interval Notation: (4, +∞)

x ≤ 4
Solution:
Step 1. Graph the solution. Use a closed dot at 4 and shade all real numbers below 4, including 4. Put negative infinity above to indicate that the solution set is unbounded to the left of the number line (or all negative real numbers).
Step 2. Write the interval notation. Use a parenthesis with the lower-bound (-∞) and a square bracket with the upper-bound (4).
Interval Notation: (-∞, 4]

Practice Writing & Graphing Interval Notation:

Graph and determine the interval notation of the following inequalities.

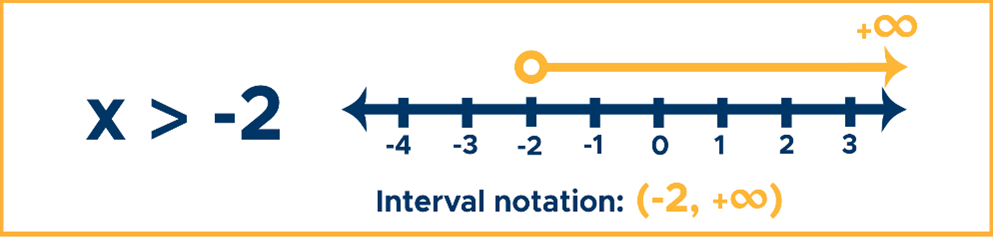
Example #1: x > -2

Solution: Use an open dot at -2 and shade all real numbers greater than -2. Use positive infinity (+∞) to mean that the solution set is unbounded to the right of the number line.
Answer: (-2, +∞)

Example 1 Graph

Example #2: x < 9

Solution: Use an open dot at 9 and shade all real numbers less than 9. Use negative infinity (-∞) to mean that the solution set is unbounded to the left of the number line.
Answer: (-∞, 9)

Example 2 Graph

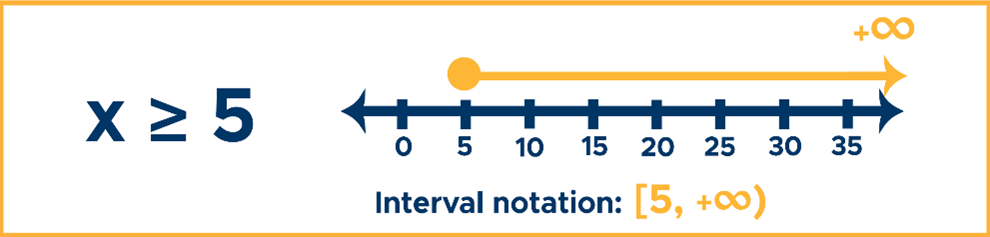
Example #3: x ≥ 5

Solution: Use a closed dot at 5 and shade all real numbers including 5 and above. Use positive infinity (+∞) to mean that the solution set is unbounded to the right of the number line.
Answer: [5, +∞)

Example 3 Graph

Example #4: x < 2 or x ≥ 8

This is an example of a compound inequality whose solutions are found in all the elements contained in the solution sets of each inequality. They are usually joined by the words "or" or "and." Combining these individual sets is called the union, symbolized by U.

Solution:

  1. First, use an open dot at 2 and shade all real numbers less than 2. Then, use negative infinity (-∞) to indicate that the solution set is unbounded to the left of the number line.
  2. Use a closed dot at 8 and shade all real numbers including 8 and above. Lastly, use positive infinity (+∞) to indicate that the solution set is unbounded to the right of the number line.
  3. Combine the interval notations using the symbol U.

Answer: (-∞, 2) U [8, +∞)

Example 4 Graph

Example #5: x ≥ 4 or x ≤ 12

Solution:

  1. First, use a closed dot at 4 and shade all real numbers including 4 and above. Use positive infinity (+∞) to indicate that the solution set is unbounded to the right of the number line.
  2. Then, use a closed dot at 12 and shade all real numbers including 12 and below. Finally, use negative infinity (-∞) to indicate that the solution set is unbounded to the left of the number line.
  3. Look at the graph to see how the lines overlap, giving us all real numbers as solutions to the inequality. Write positive and negative infinity or R in the interval notation.

Answer: R = (-∞, +∞)

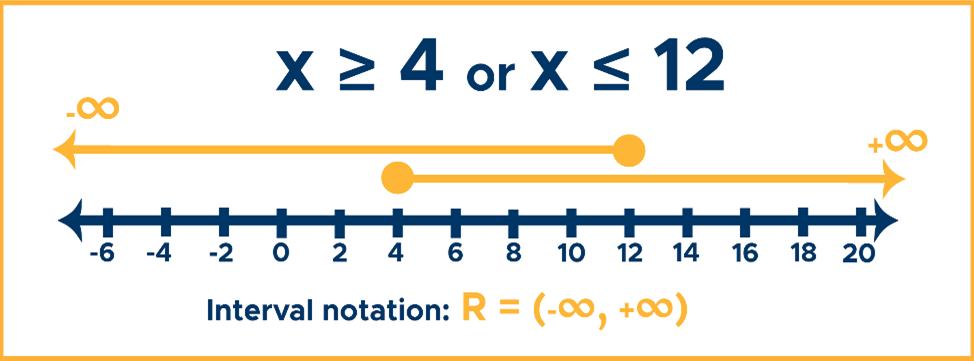
Example 5 Graph

Thank you for reading. We hope it's effective! Always feel free to revisit this page if you ever have any questions aboutinterval notation.

Check out some of our other blog posts or invest in your future with one of our self-study courses!

If you enjoyed learning about interval notation, you may be interested in our Calculus AB 2021 AP Exam Study Guide.
Click here for the Calculus AB 2021 AP Exam Study Guide!
If you enjoyed learning about interval notation, you may be interested in our Calculus BC 2021 AP Exam Study Guide.
Click here for the Calculus BC 2021 AP Exam Study Guide!